- 2017 Maps of sparse memory networks reveal overlapping communities in network flows
- 2014 Community detection and visualization of networks with the map equation framework
- 2017 Mapping higher-order network flows in memory and multilayer networks with Infomap
- 2008 Maps of information flow reveal community structure in complex networks
- 2009 The map equation
- 2010 Mapping change in large networks
- 2011 Multilevel compression of random walks on networks reveals hierarchical organization in large integrated systems
- 2011 Compression of flow can reveal overlapping modular organization in networks
- 2012 Ranking and clustering of nodes in networks with smart teleportation
- 2014 Memory in network flows and its effects on spreading dynamics and community detection
- 2015 Estimating the resolution limit of the map equation in community detection
- 2015 Identifying modular flows on multilayer networks reveals highly overlapping organization in interconnected systems
- 2016 Efficient community detection of network flows for varying Markov times and bipartite networks
- 2016 Maps of sparse Markov chains efficiently reveal community structure in network flows with memory
- 2017 Infomap Bioregions: Interactive mapping of biogeographical regions from species distributions
- 2018 Constrained information flows in temporal networks reveal intermittent communities
- 2019 Exploring the solution landscape enables more reliable network community detection
- 2019 Map equation with metadata: Varying the role of attributes in community detection
- 2020 Mapping flows on sparse networks with missing links
- 2020 Mapping flows on bipartite networks
- 2021 Identifying flow modules in ecological networks using Infomap
- 2021 How choosing random-walk model and network representation matters for flow-based community detection in hypergraphs
- 2021 Flow-based community detection in hypergraphs
- 2021 Mapping nonlocal relationships between metadata and network structure with metadata-dependent encoding of random walks
- 2021 Mapping flows on weighted and directed networks with incomplete observations
- 2022 Map Equation Centrality: Community-aware Centrality based on the Map Equation
- 2022 Similarity-based Link Prediction from Modular Compression of Network Flows
Presentations
Tutorials
Research papers
Abstracts and related figures
Maps of information flow reveal community structure in complex networks Martin Rosvall and Carl T. Bergstrom PNAS 105, 1118 (2008) [pdf]. [arXiv:0707.0609]
To comprehend the multipartite organization of large-scale
biological and social systems, we introduce a new
information-theoretic approach to reveal community structure in
weighted and directed networks. The method decomposes a network
into modules by optimally compressing a description of information
flows on the network. The result is a map that both simplifies and
highlights the regularities in the structure and their
relationships to each other. We illustrate the method by making a
map of scientific communication as captured in the citation
patterns of more than 6000 journals. We discover a multicentric
organization with fields that vary dramatically in size and degree
of integration into the network of science. Along the backbone of
the network — which includes physics, chemistry, molecular
biology, and medicine — information flows bidirectionally, but the
map reveals a directional pattern of citation from the applied
fields to the basic sciences.

The map equation Martin Rosvall, Daniel Axelsson and Carl T. Bergstrom Eur. Phys. J. Special Topics 178, 13 (2009) [pdf]. [arXiv:0906.1405]
Many real-world networks are so large that we must simplify their
structure before we can extract useful information about the
systems they represent. As the tools for doing these
simplifications proliferate within the network literature,
researchers would benefit from some guidelines about which of the
so-called community detection algorithms are most appropriate for
the structures they are studying and the questions they are
asking. Here we show that different methods highlight different
aspects of a network's structure and that the the sort of
information that we seek to extract about the system must guide us
in our decision. For example, many community detection algorithms,
including the popular modularity maximization approach, infer
module assignments from an underlying model of the network
formation process. However, we are not always as interested in how
a system's network structure was formed, as we are in how a
network's extant structure influences the system's behavior. To
see how structure influences current behavior, we will recognize
that links in a network induce movement across the network and
result in system-wide interdependence. In doing so, we explicitly
acknowledge that most networks carry flow. To highlight and
simplify the network structure with respect to this flow, we use
the map equation. We present an intuitive derivation of this
flow-based and information-theoretic method and provide an
interactive on-line application that anyone can use to explore the
mechanics of the map equation. The differences between the map
equation and the modularity maximization approach are not merely
conceptual. Because the map equation attends to patterns of flow
on the network and the modularity maximization approach does not,
the two methods can yield dramatically different results for some
network structures. To illustrate this and build our understanding
of each method, we partition several sample networks. We also
describe an algorithm and provide source code to efficiently
decompose large weighted and directed networks based on the map
equation.

Mapping change in large networks Martin Rosvall and Carl T. Bergstrom PLoS ONE 5(1): e8694 (2010) [pdf]. [arXiv:0812.1242]
Change is the very nature of interaction patterns in biology,
technology, economics, and science itself: The interactions within
and between organisms change; the air, ground, and sea traffic
change; the global financial flow changes; the scientific research
front changes. With increasingly available data, networks and
clustering tools have become important methods used to comprehend
instances of these large-scale structures. But blind to the
difference between noise and trends in the data, these tools alone
must fail when used to study change. Only if we can assign
significance to the partition of single networks can we
distinguish structural changes from fluctuations and assess how
much confidence we should have in the changes. Here we show that
bootstrap resampling accompanied by significance clustering
provides a solution to this problem. We use the significance
clustering to realize de Solla Price's vision of mapping the
change in science.

Multilevel compression of random walks on networks reveals hierarchical organization in large integrated systems Martin Rosvall and Carl T. Bergstrom PLoS ONE 6(4): e18209 (2011) [pdf]. [arXiv:1010.0431]
To comprehend the hierarchical organization of large integrated
systems, we introduce the hierarchical map equation that reveals
multilevel structures in networks. In this information-theoretic
approach, we exploit the duality between compression and pattern
detection; by compressing a description of a random walker as a
proxy for real flow on a network, we find regularities in the
network that induce this system-wide flow. Finding the shortest
multilevel description of the random walker therefore gives us the
best hierarchical clustering of the network — the optimal
number of levels and modular partition at each level — with
respect to the dynamics on the network. With a novel search
algorithm, we extract and illustrate the rich multilevel
organization of several large social and biological networks. For
example, from the global air traffic network we uncover countries
and continents, and from the pattern of scientific communication
we reveal more than 100 scientific fields organized in four major
disciplines: life sciences, physical sciences, ecology and earth
sciences, and social sciences. In general, we find shallow
hierarchical structures in globally interconnected systems, such
as neural networks, and rich multilevel organizations in systems
with highly separated regions, such as road networks.

Compression of flow can reveal overlapping modular organization in networks Alcides Viamontes Esquivel and Martin Rosvall Phys. Rev. X 1, 021025 (2011) [pdf]. [arXiv:1105.0812]
To better understand the organization of overlapping modules in
large networks with respect to flow, we introduce the map equation
for overlapping modules. In this information-theoretic framework,
we use the correspondence between compression and regularity
detection. The generalized map equation measures how well we can
compress a description of flow in the network when we partition it
into modules with possible overlaps. When we minimize the
generalized map equation over overlapping network partitions, we
detect modules that capture flow and determine which nodes at the
boundaries between modules should be classified in multiple
modules and to what degree. With a novel greedy-search algorithm,
we find that some networks, for example, the neural network of the
nematode Caenorhabditis elegans, are best described by modules
dominated by hard boundaries, but that others, for example, the
sparse European-roads network, have an organization of highly
overlapping modules.

Ranking and clustering of nodes in networks with smart teleportation Renaud Lambiotte and Martin Rosvall Phys. Rev. E 85, 056107 (2012) [pdf]. [arXiv:1112.5252]
Random teleportation is a necessary evil for ranking and
clustering directed networks based on random walks. Teleportation
enables ergodic solutions, but the solutions must necessarily
depend on the exact implementation and parametrization of the
teleportation. For example, in the commonly used PageRank
algorithm, the teleportation rate must trade off a heavily biased
solution with a uniform solution. Here we show that teleportation
to links rather than nodes enables a much smoother trade-off and
effectively more robust results. We also show that, by not
recording the teleportation steps of the random walker, we can
further reduce the effect of teleportation with dramatic effects
on clustering.

Memory in network flows and its effects on spreading dynamics and community detection Martin Rosvall, Alcides V. Esquivel, Andrea Lancichinetti, Jevin D. West, and Renaud Lambiotte Nature Comm. 5, 4630 (2014) [pdf]. [arXiv:1305.4807] [data] « Interactive storyboard »
Random walks on networks is the standard tool for modelling
spreading processes in social and biological systems. This
first-order Markov approach is used in conventional community
detection, ranking and spreading analysis, although it ignores a
potentially important feature of the dynamics: where flow moves to
may depend on where it comes from. Here we analyse pathways from
different systems, and although we only observe marginal
consequences for disease spreading, we show that ignoring the
effects of second-order Markov dynamics has important consequences
for community detection, ranking and information spreading. For
example, capturing dynamics with a second-order Markov model
allows us to reveal actual travel patterns in air traffic and to
uncover multidisciplinary journals in scientific communication.
These findings were achieved only by using more available data and
making no additional assumptions, and therefore suggest that
accounting for higher-order memory in network flows can help us
better understand how real systems are organized and function.

Estimating the resolution limit of the map equation in community detection Tatsuro Kawamoto and Martin Rosvall Phys Rev E 91, 012809 (2015) [pdf]. [arXiv:1402.4385]
A community detection algorithm is considered to have a resolution
limit if the scale of the smallest modules that can be resolved
depends on the size of the analyzed subnetwork. The resolution
limit is known to prevent some community detection algorithms from
accurately identifying the modular structure of a network. In
fact, any global objective function for measuring the quality of a
two-level assignment of nodes into modules must have some sort of
resolution limit or an external resolution parameter. However, it
is yet unknown how the resolution limit affects the so-called map
equation, which is known to be an efficient objective function for
community detection. We derive an analytical estimate and conclude
that the resolution limit of the map equation is set by the total
number of links between modules instead of the total number of
links in the full network as for modularity. This mechanism makes
the resolution limit much less restrictive for the map equation
than for modularity; in practice, it is orders of magnitudes
smaller. Furthermore, we argue that the effect of the resolution
limit often results from shoehorning multilevel modular structures
into two-level descriptions. As we show, the hierarchical map
equation effectively eliminates the resolution limit for networks
with nested multilevel modular structures.

Identifying modular flows on multilayer networks reveals highly overlapping organization in interconnected systems Manlio De Domenico, Andrea Lancichinetti, Alex Arenas, and Martin Rosvall Phys Rev X 5, 011027 (2015) [pdf]. [arXiv:1408.2925] « Interactive storyboard »
To comprehend interconnected systems across the social and natural
sciences, researchers have developed many powerful methods to
identify functional modules. For example, with interaction data
aggregated into a single network layer, flow-based methods have
proven useful for identifying modular dynamics in weighted and
directed networks that capture constraints on flow processes.
However, many interconnected systems consist of agents or
components that exhibit multiple layers of interactions, possibly
from several different processes. Inevitably, representing this
intricate network of networks as a single aggregated network leads
to information loss and may obscure the actual organization. Here,
we propose a method based on a compression of network flows that
can identify modular flows both within and across layers in
nonaggregated multilayer networks. Our numerical experiments on
synthetic multilayer networks, with some layers originating from
the same interaction process, show that the analysis fails in
aggregated networks or when treating the layers separately,
whereas the multilayer method can accurately identify modules
across layers that originate from the same interaction process. We
capitalize on our findings and reveal the community structure of
two multilayer collaboration networks with topics as layers:
scientists affiliated with the Pierre Auger Observatory and
scientists publishing works on networks on the arXiv. Compared to
conventional aggregated methods, the multilayer method uncovers
connected topics and reveals smaller modules with more overlap
that better capture the actual organization.

Efficient community detection of network flows for varying Markov times and bipartite networks Masoumeh Kheirkhahzadeh, Andrea Lancichinetti, and Martin Rosvall Phys. Rev. E 93, 032309 (2016) [pdf]. [arXiv:1511.01540]
Community detection of network flows conventionally assumes
one-step dynamics on the links. For sparse networks and interest
in large-scale structures, longer timescales may be more
appropriate. Oppositely, for large networks and interest in
small-scale structures, shorter timescales may be better. However,
current methods for analyzing networks at different timescales
require expensive and often infeasible network reconstructions. To
overcome this problem, we introduce a method that takes advantage
of the inner-workings of the map equation and evades the
reconstruction step. This makes it possible to efficiently analyze
large networks at different Markov times with no extra overhead
cost. The method also evades the costly unipartite projection for
identifying flow modules in bipartite networks.

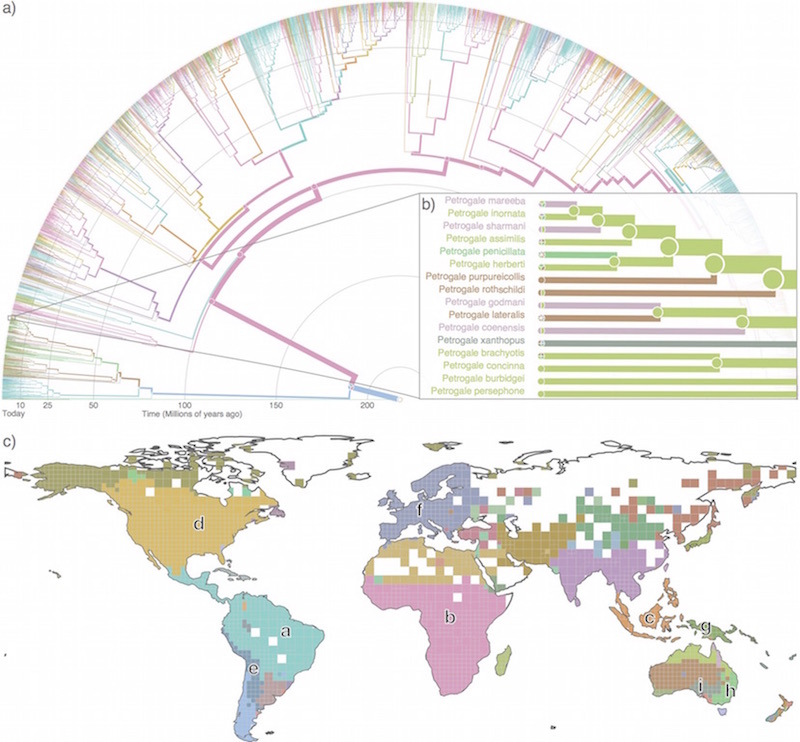
Infomap Bioregions: Interactive mapping of biogeographical regions from species distributions Daniel Edler, Thaís Guedes, Alexander Zizka, Martin Rosvall, and Alexandre Antonelli Syst. Biol. 66 (2): 197-204 (2017) [pdf]. [arXiv:1512.00892] « Interactive mapping tool »
Biogeographical regions (bioregions) reveal how different sets of
species are spatially grouped and therefore are important units
for conservation, historical biogeography, ecol- ogy and
evolution. Several methods have been developed to identify
bioregions based on species distribution data rather than expert
opinion. One approach successfully applies network theory to
simplify and highlight the underlying structure in species
distributions. However, this method lacks tools for simple and
efficient analysis. Here we present In- fomap Bioregions, an
interactive web application that inputs species distribution data
and generates bioregion maps. Species distributions may be
provided as georeferenced point occurrences or range maps, and can
be of local, regional or global scale. The application uses a
novel adaptive resolution method to make best use of often
incomplete species dis- tribution data. The results can be
downloaded as vector graphics, shapefiles or in table format. We
validate the tool by processing large datasets of publicly
available species distribution data of the world’s amphibians
using species ranges, and mammals using point occurrences. As
examples of applications, researchers can reconstruct ancestral
ranges in historical biogeography or identify indicator species
for targeted conservation.
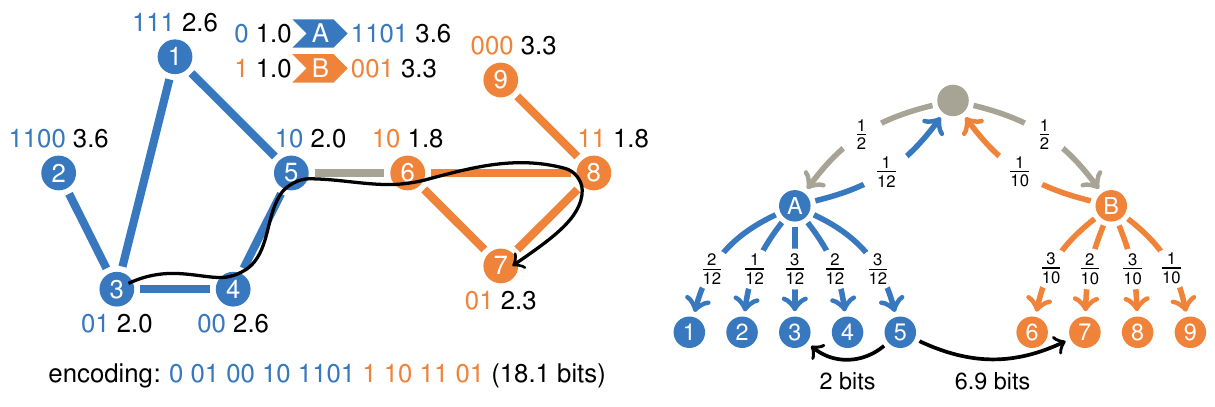
Maps of sparse Markov chains efficiently reveal community structure in network flows with memory Christian Persson, Ludvig Bohlin, Daniel Edler, and Martin Rosvall [pdf]. [arXiv:1606.08328] « Interactive map of sparse Markov chains »
To better understand the flows of ideas or information through
social and biological systems, researchers develop maps that
reveal important patterns in network flows. In practice, network
flow models have implied memoryless first-order Markov chains, but
recently researchers have introduced higher-order Markov chain
models with memory to capture patterns in multi-step pathways.
Higher-order models are particularly important for effectively
revealing actual, overlapping community structure, but
higher-order Markov chain models suffer from the curse of
dimensionality: their vast parameter spaces require exponentially
increasing data to avoid overfitting and therefore make mapping
inefficient already for moderate-sized systems. To overcome this
problem, we introduce an efficient cross-validated mapping
approach based on network flows modeled by sparse Markov chains.
To illustrate our approach, we present a map of citation flows in
science with research fields that overlap in multidisciplinary
journals. Compared with currently used categories in science of
science studies, the research fields form better units of analysis
because the map more effectively captures how ideas flow through
science.

Mapping higher-order network flows in memory and multilayer networks with Infomap Daniel Edler, Ludvig Bohlin, and Martin Rosvall Algorithms 10, 112 (2017) [pdf]. [arXiv:1706.04792] « Interactive map of sparse Markov chains »
Comprehending complex systems by simplifying and highlighting
important dynamical patterns requires modeling and mapping
higher-order network flows. However, complex systems come in
many forms and demand a range of representations, including
memory and multilayer networks, which in turn call for versatile
community-detection algorithms to reveal important modular
regularities in the flows. Here we show that various forms of
higher-order network flows can be represented in a unified way
with networks that distinguish physical nodes for representing
a complex system’s objects from state nodes for describing
flows between the objects. Moreover, these so-called sparse
memory networks allow the information-theoretic community
detection method known as the map equation to identify
overlapping and nested flow modules in data from a range of
different higher-order interactions such as multistep,
multi-source, and temporal data. We derive the map equation
applied to sparse memory networks and describe its search
algorithm Infomap, which can exploit the flexibility of
sparse memory networks. Together they provide a general
solution to reveal overlapping modular patterns in higher-order
flows through complex systems.

Constrained information flows in temporal networks reveal intermittent communities Ulf Aslak, Martin Rosvall, and Sune Lehmann Phys. Rev. E 97, 062312 (2018) [pdf]. [arXiv:1711.07649] « Interactive visualization of intermittent communities »
Many real-world networks are representations of dynamic systems
with interactions that change over time, often in uncoordinated
ways and at irregular intervals. For example, university students
connect in intermittent groups that repeatedly form and dissolve
based on multiple factors, including their lectures, interests,
and friends. Such dynamic systems can be represented as multilayer
networks where each layer represents a snapshot of the temporal
network. In this representation, it is crucial that the links
between layers accurately capture real dependencies between those
layers. Often, however, these dependencies are unknown. Therefore,
current methods connect layers based on simplistic assumptions
that cannot capture node-level layer dependencies. For example,
connecting every node to itself in other layers with the same
weight can wipe out essential dependencies between intermittent
groups, making it difficult or even impossible to identify them.
In this paper, we present a principled approach to estimating
node-level layer dependencies based on the network structure
within each layer. We implement our node-level coupling method in
the community detection framework Infomap and demonstrate its
performance compared to current methods on synthetic and real
temporal networks. We show that our approach more effectively
constrains information inside multilayer communities so that
Infomap can better recover planted groups in multilayer benchmark
networks that represent multiple modes with different groups and
better identify intermittent communities in real temporal contact
networks. These results suggest that node-level layer coupling can
improve the modeling of information spreading in temporal networks
and better capture their dynamic community structure.

Exploring the solution landscape enables more reliable network community detection Joaquín Calatayud, Rubén Bernardo-Madrid, Magnus Neuman, Alexis Rojas, and Martin Rosvall Phys. Rev. E 100, 052308 (2019) [pdf]. [arXiv:1905.11230] « Code available on GitHub »
To understand how a complex system is organized and functions,
researchers often identify communities in the system's network of
interactions. Because it is practically impossible to explore all
solutions to guarantee the best one, many community-detection
algorithms rely on multiple stochastic searches. But for a given
combination of network and stochastic algorithm, how many searches
are sufficient to find a solution that is good enough? The
standard approach is to pick a reasonably large number of searches
and select the network partition with the highest quality or
derive a consensus solution based on all network partitions.
However, if different partitions have similar qualities such that
the solution landscape is degenerate, the single best partition
may miss relevant information, and a consensus solution may blur
complementary communities. Here we address this degeneracy problem
with coarse-grained descriptions of the solution landscape. We
cluster network partitions based on their similarity and suggest
an approach to determine the minimum number of searches required
to describe the solution landscape adequately. To make good use of
all partitions, we also propose different ways to explore the
solution landscape, including a significance clustering procedure.
We test these approaches on synthetic and real-world networks, and
find that different networks and algorithms require a different
number of searches and that exploring the coarse-grained solution
landscape can reveal noteworthy complementary solutions and enable
more reliable community detection.

Map equation with metadata: Varying the role of attributes in
community detection
Scott Emmons and Peter J. Mucha
Phys. Rev. E 100, 022301 (2019)
[pdf]. [arXiv:1810.10433]
« Infomap v1.0 options:
--meta-data <p> --meta-data-rate <f>
»
Much of the community detection literature studies structural
communities, communities defined solely by the connectivity
patterns of the network. Often networks contain additional
metadata which can inform community detection such as the grade
and gender of students in a high school social network. In this
work, we introduce a tuning parameter to the content map equation
that allows users of the Infomap community detection algorithm to
control the metadata’s relative importance for identifying network
structure. On synthetic networks, we show that our algorithm can
overcome the structural detectability limit when the metadata are
well aligned with community structure. On real-world networks, we
show how our algorithm can achieve greater mutual information with
the metadata at a cost in the traditional map equation. Our tuning
parameter, like the focusing knob of a microscope, allows users to
“zoom in” and “zoom out” on communities with varying levels of
focus on the metadata.

Mapping flows on sparse networks with missing links
Jelena Smiljanić, Daniel Edler, and Martin Rosvall
Phys. Rev. E 102, 012302 (2020)
[pdf]. [arXiv:1912.05377]
« Infomap v1/bayes option:
--bayes
»
Unreliable network data can cause community-detection methods to overfit and highlight spurious structures with misleading information about the organization and function of complex systems. Here we show how to detect significant flow-based communities in sparse networks with missing links using the map equation. Since the map equation builds on Shannon entropy estimation, it assumes complete data such that analyzing undersampled networks can lead to overfitting. To overcome this problem, we incorporate a Bayesian approach with assumptions about network uncertainties into the map equation framework. Results in both synthetic and real-world networks show that the Bayesian estimate of the map equation provides a principled approach to revealing significant structures in undersampled networks.
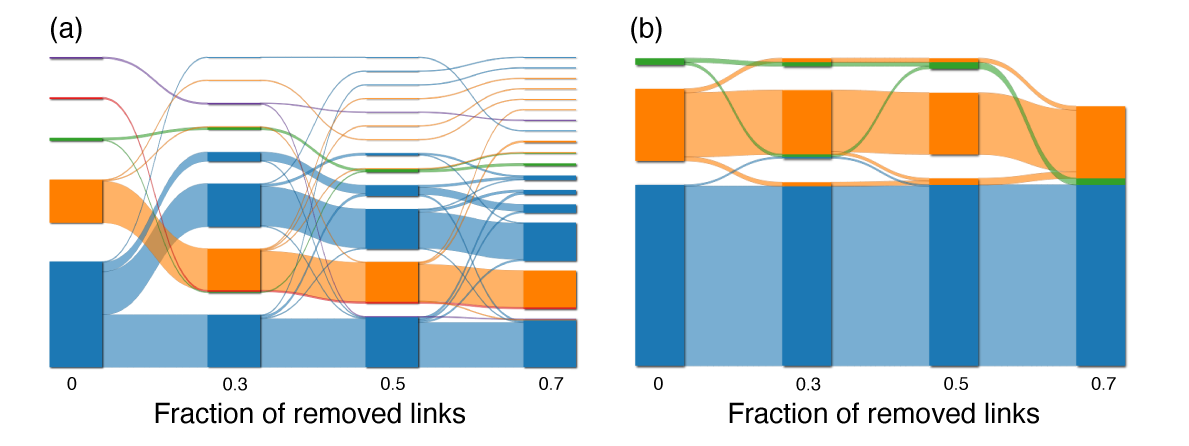
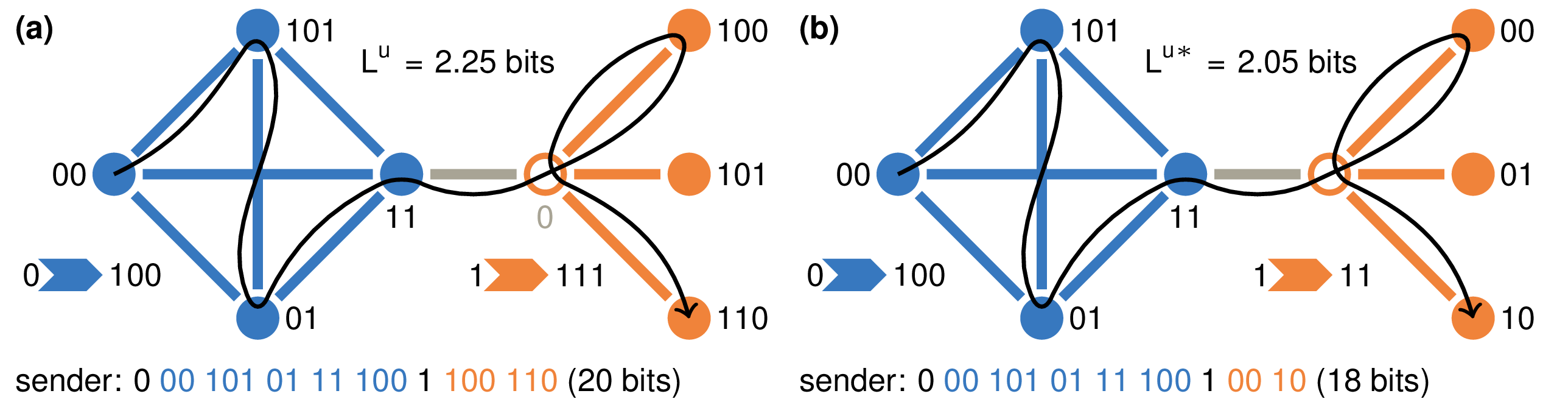
Mapping flows on bipartite networks Christopher Blöcker, Martin Rosvall Phys. Rev. E 102, 052305 (2020) [pdf]. [arXiv:2007.01666] « Bipartite Infomap »
Mapping network flows provides insight into the organization of networks, but even though many real-networks are bipartite, no method for mapping flows takes advantage of the bipartite structure. What do we miss by discarding this information and how can we use it to understand the structure of bipartite networks better? The map equation models network flows with a random walk and exploits the information-theoretic duality between compression and finding regularities to detect communities in networks. However, it does not use the fact that random walks in bipartite networks alternate between node types, information worth 1 bit. To make some or all of this information available to the map equation, we developed a coding scheme that remembers node types at different rates. We explored the community landscape of bipartite real-world networks from no node-type information to full node-type information and found that using node types at a higher rate generally leads to deeper community hierarchies and a higher resolution. The corresponding compression of network flows exceeds the amount of extra information provided. Consequently, taking advantage of the bipartite structure increases the resolution and reveals more network regularities.
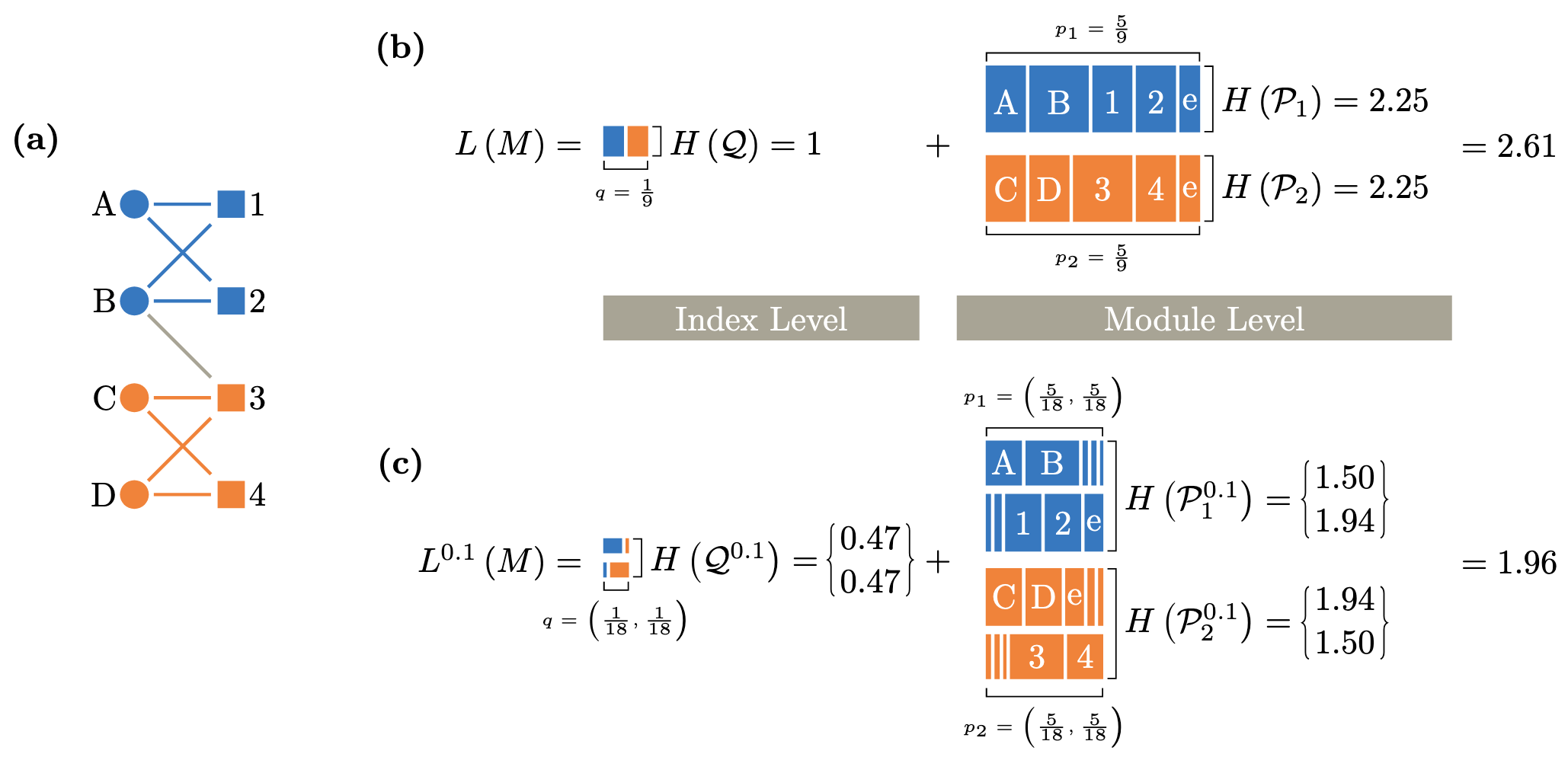
Identifying flow modules in ecological networks using Infomap Carmel Farage, Daniel Edler, Anna Eklöf, Martin Rosvall, and Shai Pilosof Methods Ecol Evol. 2021;12:778-786 [pdf]. [bioRxiv:2020.04.14] « Documentation »
- Analysing how species interact in modules is a fundamental problem in network ecology. Theory shows that a modular network structure can reveal underlying dynamic ecological and evolutionary processes, influence dynamics that operate on the network and affect the stability of the ecological system.
- Although many ecological networks describe flows, such as biomass flows in food webs or disease transmission, most modularity analyses have ignored network flows, which can hinder our understanding of the interplay between structure and dynamics.
- Here we present Infomap, an established method based on network flows to the field of ecological networks. Infomap is a flexible tool that can identify modules in virtually any type of ecological network and is particularly useful for directed, weighted and multilayer networks. We illustrate how Infomap works on all these network types. We also provide a fully documented repository with additional ecological examples. Finally, to help researchers to analyse their networks with Infomap, we introduce the open-source R package infomapecology.
- Analysing flow-based modularity is useful across ecology and transcends to other biological and non-biological disciplines. A dynamic approach for detecting modu- lar structure has strong potential to provide new insights into the organisation of ecological networks.

How choosing random-walk model and network representation matters for flow-based community detection in hypergraphs Anton Eriksson, Daniel Edler, Alexis Rojas, Manlio de Domenico, and Martin Rosvall Comm. Phys. 4, 133 (2021) [pdf]. [arXiv:2101.00656] « Code on GitHub »
Hypergraphs offer an explicit formalism to describe multibody interactions in complex systems. To connect dynamics and function in systems with these higher-order interactions, network scientists have generalised random-walk models to hypergraphs and studied the multibody effects on flow-based centrality measures. But mapping the large-scale structure of those flows requires effective community detection methods. We derive unipartite, bipartite, and multilayer network representations of hypergraph flows and explore how they and the underlying random-walk model change the number, size, depth, and overlap of identified multilevel communities. These results help researchers choose the appropriate modelling approach when mapping flows on hypergraphs.
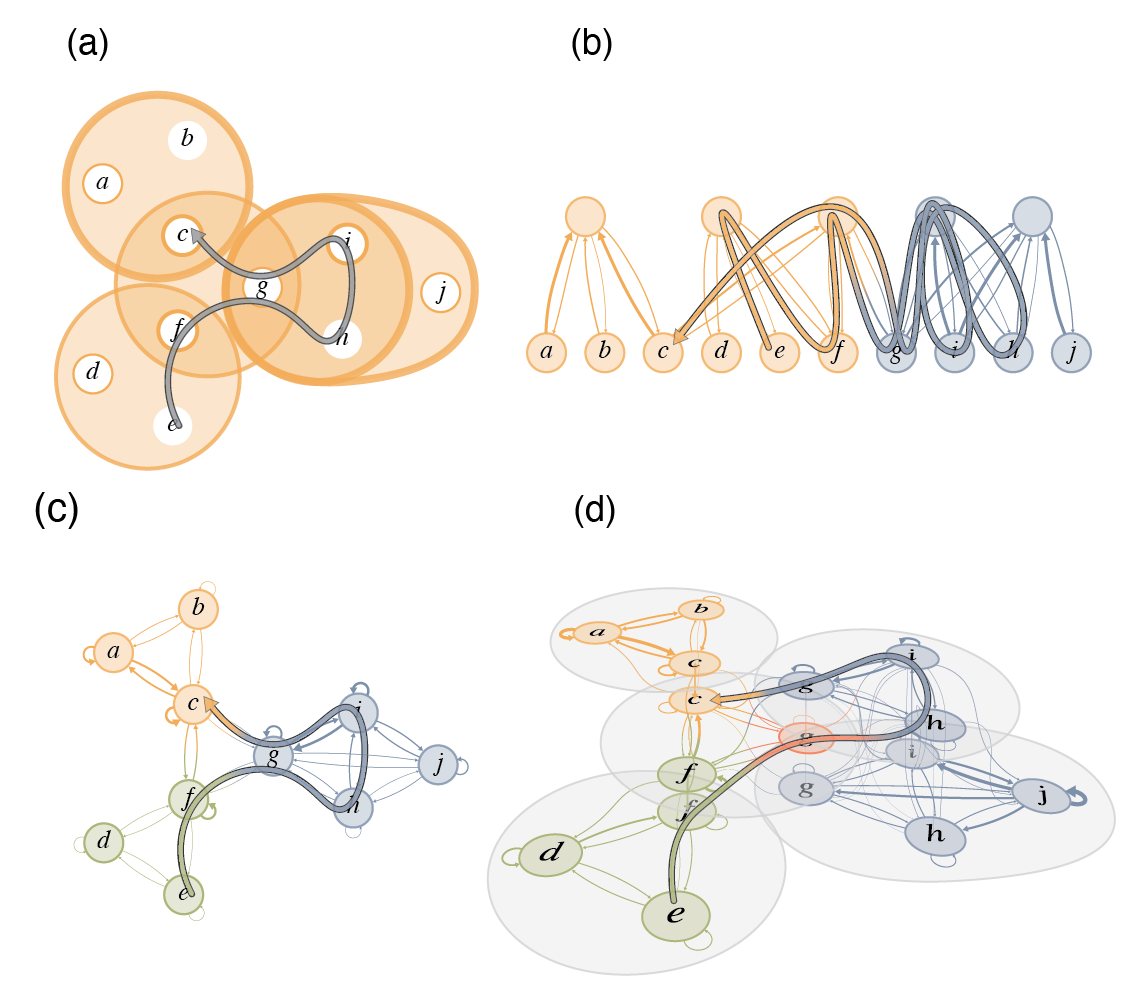
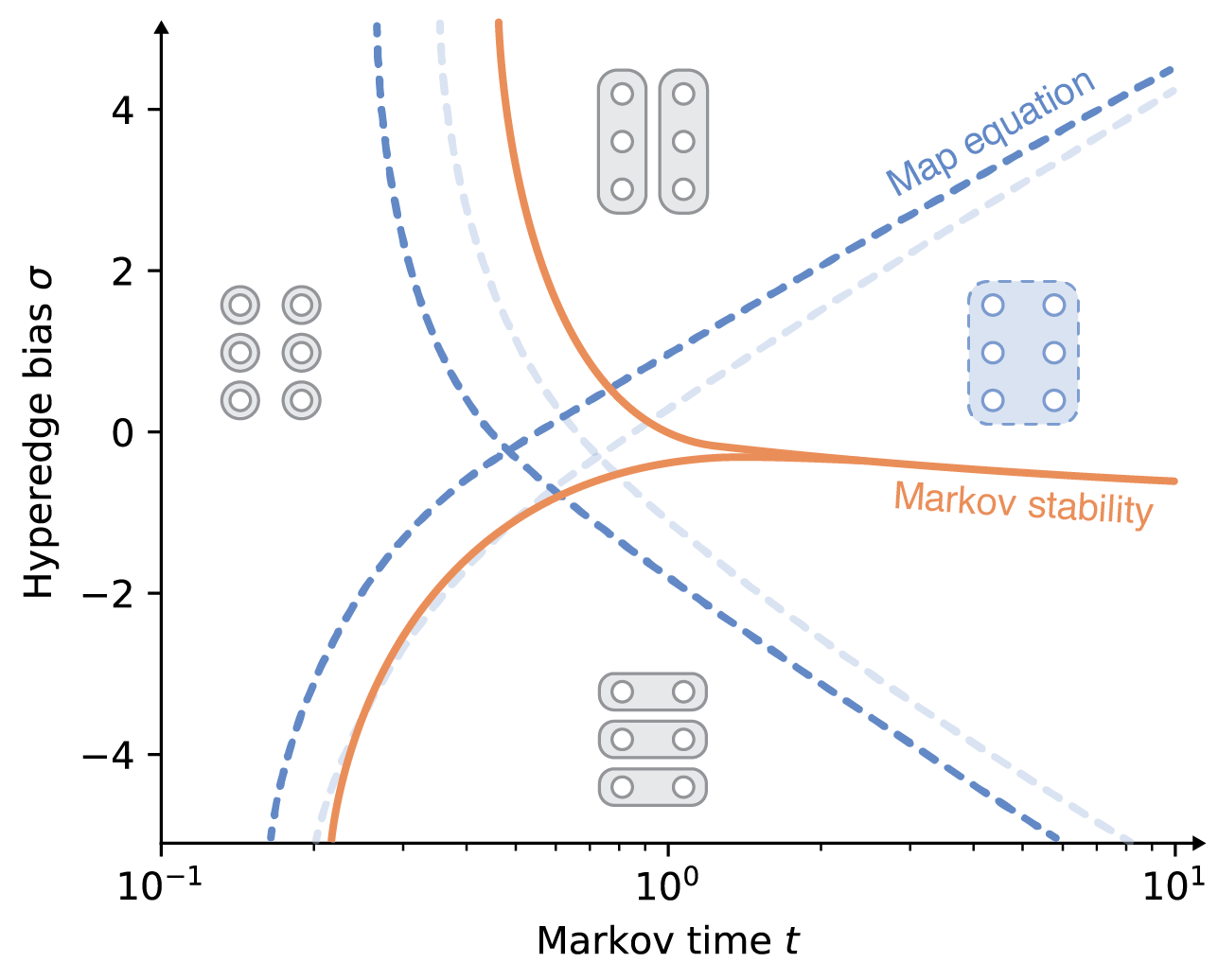
Flow-based community detection in hypergraphs Anton Eriksson, Timoteo Carletti, Renaud Lambiotte, Alexis Rojas, and Martin Rosvall [arXiv:2105.04389]
To connect structure, dynamics and function in systems with multibody interactions, network scientists model
random walks on hypergraphs and identify communities that confine the walks for a long time.
The two flow-based community-detection methods Markov stability and the map equation identify such communities
based on different principles and search algorithms. But how similar are the resulting communities? We explain
both methods' machinery applied to hypergraphs and compare them on synthetic and real-world hypergraphs using
various hyperedge-size biased random walks and time scales. We find that the map equation is more sensitive to
time-scale changes and that Markov stability is more sensitive to hyperedge-size biases.
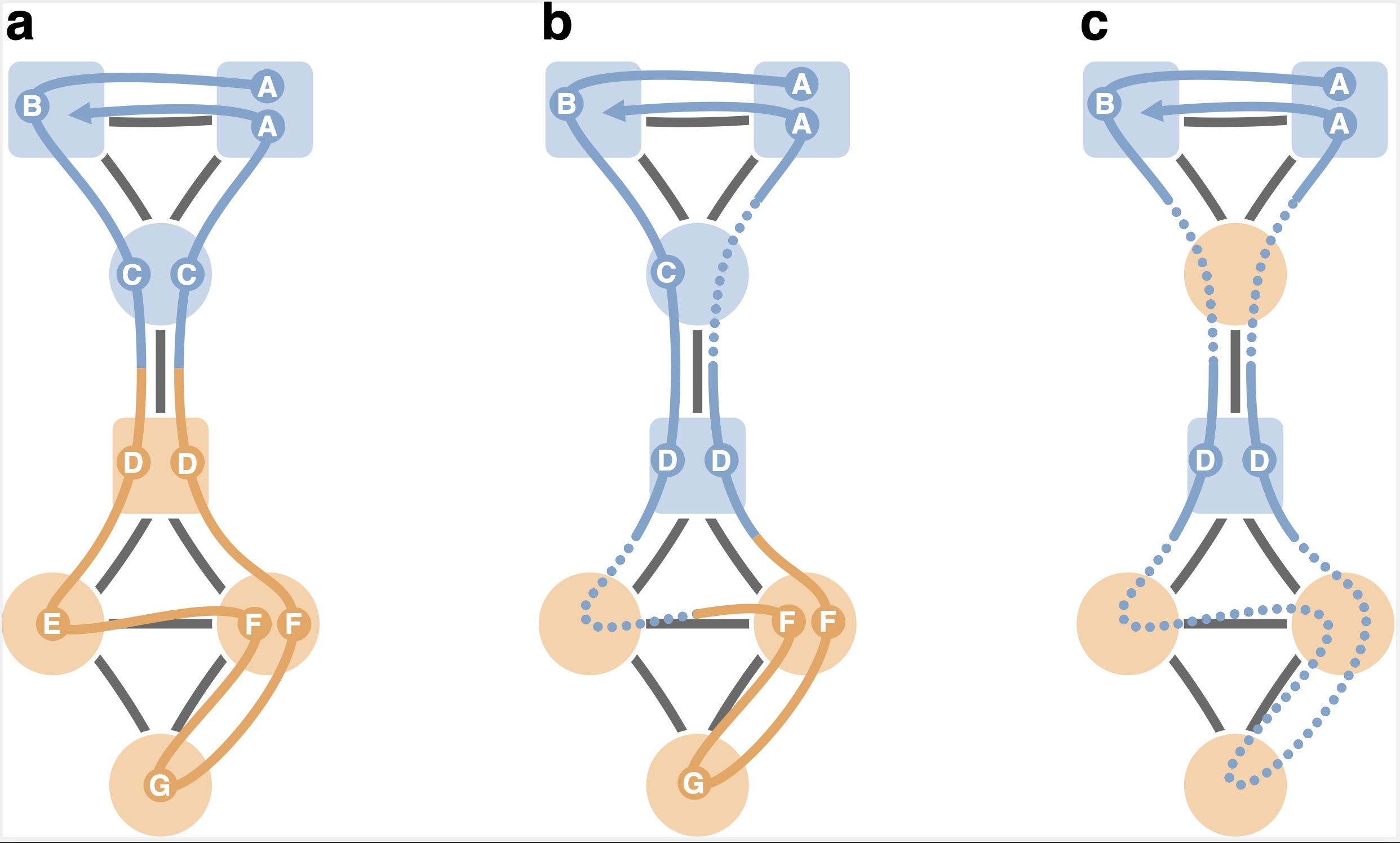
Mapping nonlocal relationships between metadata and network structure with metadata-dependent encoding of random walks Aleix Bassolas, Anton Holmgren, Antoine Marot, Martin Rosvall, Vincenzo Nicosia Sci. Adv. 8, 43 (2022) [pdf]. [arXiv:2111.05158]
Integrating structural information and metadata, such as gender,
social status, or interests, enriches networks and enables a better
understanding of the large-scale structure of complex
systems. However, existing metadata integration approaches
consider only immediately adjacent nodes, thus failing to identify
and exploit non-local relations between metadata and network
structure, typical of many spatial and social
systems. We show how a flow-based community-detection approach can integrate
network information and distant metadata, revealing more complex relations. We analyze social and
spatial networks using the map equation framework and find that
our methodology can detect functional metadata-informed
communities in diverse real-world systems. For example, in a mobility network of London, we identify communities that
reflect the income distribution, and in a European power-grid network, we identify communities that capture relations
between geography and energy prices beyond country borders.
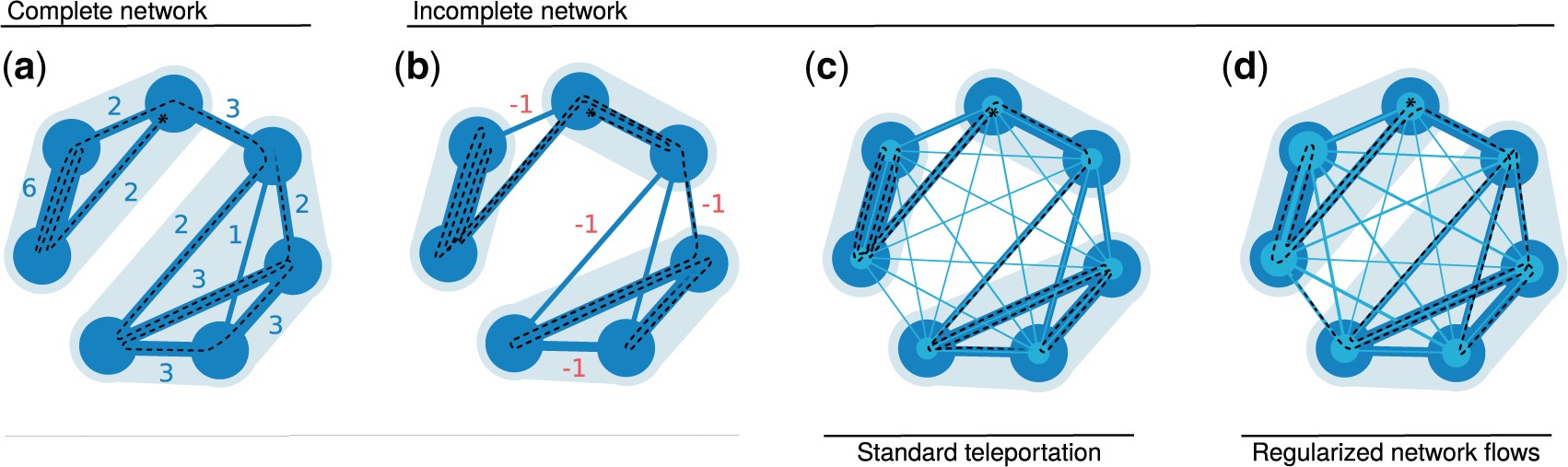
Mapping flows on weighted and directed networks with incomplete observations Jelena Smiljanić, Christopher Blöcker, Daniel Edler, Martin Rosvall J. Comp. Net. 9, 6 (2021) [pdf]. [arXiv:2106.14798]
Detecting significant community structure in networks with incomplete observations is challenging because the evidence
for specific solutions fades away with missing data. For example, recent research shows that flow-based community
detection methods can highlight spurious communities in sparse undirected and unweighted networks with missing links.
Current Bayesian approaches developed to overcome this problem do not work for incomplete observations in weighted and
directed networks that describe network flows. To overcome this gap, we extend the idea behind the Bayesian estimate of
the map equation for unweighted and undirected networks to enable more robust community detection in weighted and
directed networks. We derive an empirical Bayes estimate of the transitions rates that can incorporate metadata
information and show how an efficient implementation in the community-detection method Infomap provides more reliable
communities even with a significant fraction of data missing.
Map Equation Centrality: A Community-Aware Centrality Score Based on the Map Equation Christopher Blöcker, Juan Carlos Nieves, Martin Rosvall Appl Netw Sci 7, 56 (2022) [pdf] [arXiv:2201.12590]
To measure node importance, network scientists employ centrality scores that typically take a microscopic or macroscopic
perspective, relying on node features or global network structure. However, traditional centrality measures such as
degree centrality, betweenness centrality, or PageRank neglect the community structure found in real-world networks.
To study node importance based on network flows from a mesoscopic perspective, we analytically derive a community-aware
information-theoretic centrality score based on network flow and the coding principles behind the map equation:
map equation centrality. Map equation centrality measures how much further we can compress the network's modular
description by not coding for random walker transitions to the respective node, using an adapted coding scheme and
determining node importance from a network flow-based point of view. The information-theoretic centrality measure can
be determined from a node's local network context alone because changes to the coding scheme only affect other nodes
in the same module. Map equation centrality is agnostic to the chosen network flow model and allows researchers to
select the model that best reflects the dynamics of the process under study. Applied to synthetic networks, we
highlight how our approach enables a more fine-grained differentiation between nodes than node-local or network-global
measures. Predicting influential nodes for two different dynamical processes on real-world networks with traditional
and other community-aware centrality measures, we find that activating nodes based on map equation centrality scores
tends to create the largest cascades in a linear threshold model.
Similarity-based Link Prediction from Modular Compression of Network Flows Christopher Blöcker, Jelena Smiljanić, Ingo Scholtes, Martin Rosvall Proceedings of Machine Learning Research, PMLR 198:52:1-52:18 (2022) [pdf] [OpenReview] [arXiv:2208.14220]
Node similarity scores are a foundation for machine learning in graphs for clustering, node classification, anomaly detection,
and link prediction with applications in biological systems, information networks, and recommender systems. Recent works on
link prediction use vector space embeddings to calculate node similarities in undirected networks with good performance.
Still, they have several disadvantages: limited interpretability, need for hyperparameter tuning, manual model fitting through
dimensionality reduction, and poor performance from symmetric similarities in directed link prediction. We propose MapSim,
an information-theoretic measure to assess node similarities based on modular compression of network flows. Unlike vector
space embeddings, MapSim represents nodes in a discrete, non-metric space of communities and yields asymmetric similarities
in an unsupervised fashion. We compare MapSim on a link prediction task to popular embedding-based algorithms across 47 networks
and find that MapSim's average performance across all networks is more than 7% higher than its closest competitor, outperforming
all embedding methods in 11 of the 47 networks. Our method demonstrates the potential of compression-based approaches in graph
representation learning, with promising applications in other graph learning tasks.